テニスの試合シミュレータをつくり、錦織とジョコビッチを1000回対戦させてみました
公開日:
最終更新日:2017/09/25
2017/09/25
テニスの試合シミュレータをつくってみました。
シミュレータを使うことで、選手AとBをプログラム上で1000試合対戦させて勝ち数と負け数を計算し、どちらの選手がどのぐらいの確率で勝つかを予想することができます。
試合シミュレータをつくった理由
ランキング1位の選手と50位の選手が試合をするときに、1位の選手が勝つ可能性が高いのは想像できるのですが、
どのぐらいの確率なのかを数字で捉えることができません。
試合の確率を予測できたりすると、試合前にどのぐらい期待していいのかがわかりますし、
上位ランカーに勝ったり、下位ランカーに負けた時にそれがどのぐらい珍しいことなのかを数字で捉えることができます。
そんな考えから、
試合の確率を予想できるようなシステムがつくれたら面白いなあと前からぼんやりと思っていました。
参考にしたもの
情報収集していると、ヒントになるものがいくつかあったので、それらを参考にしてシミュレータをつくってみようと考えました。
・参考①バレーボールシミュレーション
株式会社ライツという会社がオリナスアスリートという名前でバレーボールシミュレーションをつくってるという話がリンク先の動画の中でありました。【全編動画付き】SAJ2016講演:AI(人工知能)はスポーツをどう変えるか(すいません、有料ですがスポーツのデータ分析などに興味のある方は是非みてみるといいと思います)
過去のポイントデータや選手やボールの動きを材料データとして確率分布をつくり、乱数シミュレーションによって、試合をコンピュータ上で再現するものをつくっているとありました。
作戦を試してどうなるかを仮想検証できるようにするのが狙いで、たくさんの試合数で試行錯誤できるところにメリットがあるはずだとも言っています。
ライツ社は、サッカーでも似たようなシステムをつくろうとしているみたいです。詳しくはAIでサッカーの指導はどう変わる?(ブログ nishi19 breaking news)に書いてあります。
・参考②囲碁の人工知能・モンテカルロシミュレーション
前にディープマインド社が開発した人工知能が囲碁の世界チャンピオンに勝ったことが話題になりました。ディープラーニングと強化学習が人工知能の強さのポイントとしてありますが、もうひとつモンテカルロ法が用いられたというのが工夫のポイントとしてあります。これは乱数シミュレーションによって、その後のゲームを進行させていって多くのパターンの中から最終的に勝つ確率が一番高い手を、次の手として選択していると。
・過去のデータを使う
・乱数シミュレーション
・たくさんの試合を進行させる
これらの考えを採用することで、テニスの試合シミュレータがつくれるんじゃないかと考えました。
構想・コーディング含めて1日で作成したものなので、まだ粗が目立つかと思いますが、ご容赦ください。
確率なので、外れる可能性はもちろんありますが、参考値としてでも、考える材料になったり使い道はあるかと思い、試合シミュレータをつくってみた次第です。
ディープマインド社が開発した囲碁の人工知能は、アルファ碁という名前ですが、その中身について説明された本が↓になります。
ディープラーニング(深層学習)、モンテカルロ法、強化学習などについて書かれています。前提知識がないと理解するのは辛いかもしれません。
錦織圭とノバク・ジョコビッチを1000試合対戦させてみると
249勝751敗という結果となりました。
錦織がジョコビッチに勝つ確率は24.9%と予想することができます。
4回やって1回勝てるかという確率ですが、
2016年は、0勝4敗でしたので、期待よりも悪い勝率だったと言えます。
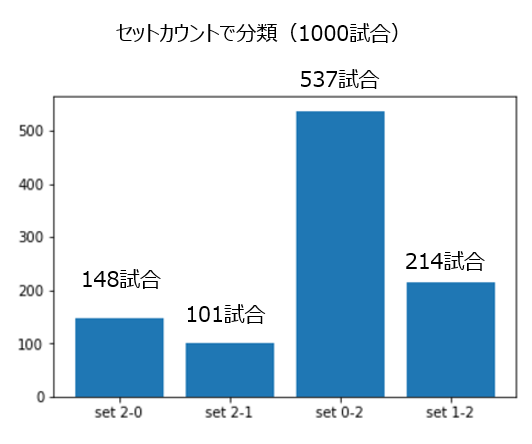
セットカウントの内容ごとに試合を分類すると、
セット2-0 148試合
セット2-1 101試合
セット0-2 537試合
セット1-2 214試合
(錦織-ジョコビッチ)
となります。
錦織がストレート(2-0)で勝つ確率は14.8%(148/1000)で、ファイナルセット(2-1)は10.1%(101/1000)と、ストレートで勝つ確率の方が高くなっているのは少し意外です。
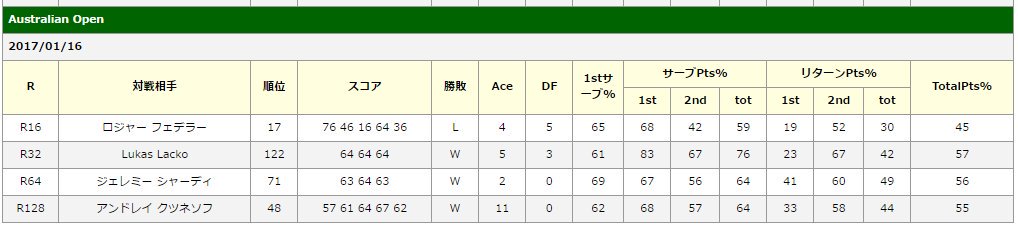
↓は予測STATSの分布データとなっています。
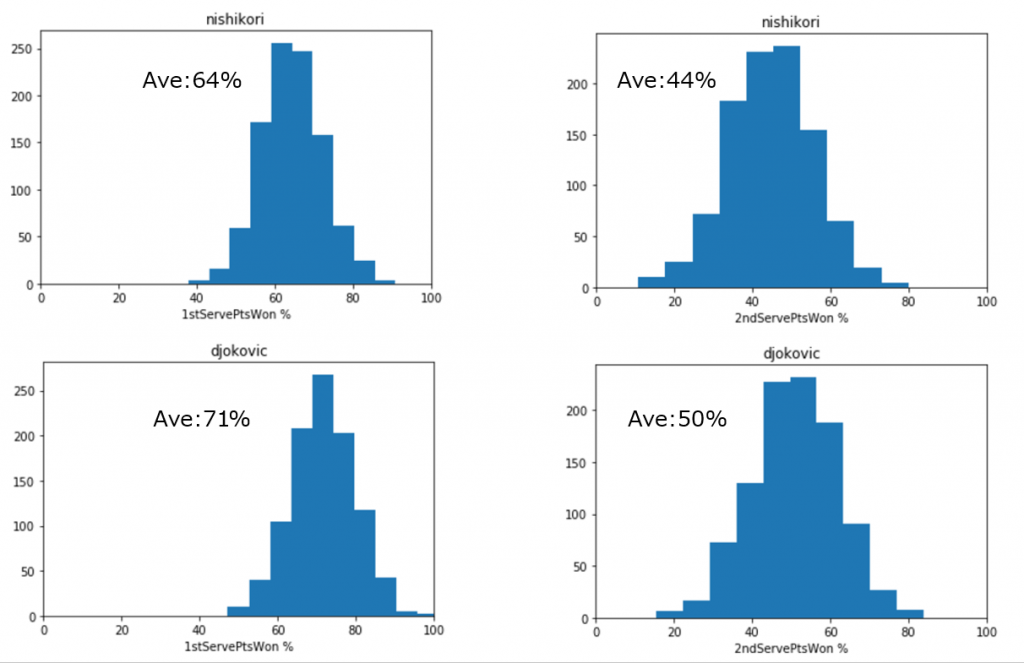
上が錦織のデータ、下がジョコビッチのデータ
左が1stサーブポイント率、右が2ndサーブポイント率となっています。
1st・2ndサーブともにポイント率がジョコビッチの方が高くなっていることがわかります。
平均値は、
1st 64%、71%(錦織、ジョコビッチ)
2nd 44%、50%(錦織、ジョコビッチ)
ただし、分布データをみてわかるようにポイント率に幅を持っているため錦織が上回る試合も少なからずあるため、
それが錦織の勝つ試合(249試合)へとつながってきます。
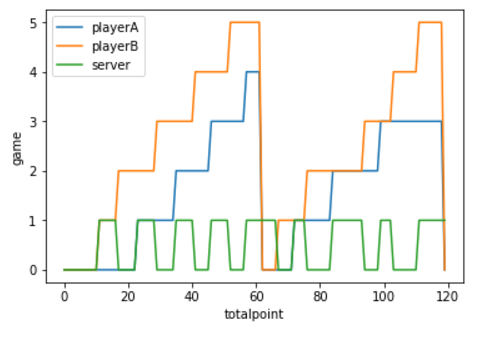
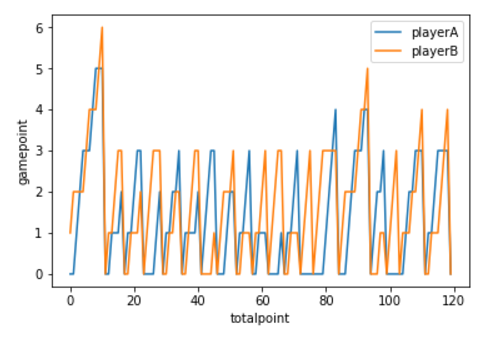
ある1試合のゲーム履歴とポイント履歴をグラフでプロットすると下のようになります。
(PlayerA:錦織、PlayerB:ジョコビッチ)
錦織から4-6、3-6でジョコビッチに負けた試合となります。
こんな感じで、全ポイントを確率データをもとに計算していっています。
そして、これを1000試合繰り返し、何勝何敗になるかを算出していきます。
シミュレータの機能について
シミュレータの機能など概要を以下に説明します。
・勝率の予想
選手A、Bどちらの選手がどのぐらいの確率で勝つのかを予想します。
(プログラム上で1000試合対戦させ、勝ち数と負け数を算出し、勝ち数を勝つ確率(%)とします)
・選手2人の年間平均STATSの掛け合わせから試合でのサーブ・リターン確率を算出(重回帰分析)
選手Aと選手Bの年間平均STATS(サーブポイント率・リターンポイント率)を掛け合わせて、その試合でのサーブ確率・リターン確率を算出します。算出には重回帰分析を用います。重回帰分析の係数決定は次で説明しますが、
1st・2ndサーブポイント率、1st・2ndリターンポイント率を変数X1、X2、X3、X4として、
その試合での1stサーブポイント率Y1と2ndサーブポイント率Y2を算出します。
式にすると、
Y1=A1・X1+A2・X2+A3・X3+A4・X4
Y2=B1・X1+B2・X2+B3・X3+B4・X4
となります。
図の表は、錦織圭とノバクジョコビッチの平均STATSを掛け合わせた場合の予想STATSとなります。
お互い2ndリターンポイント率が高い選手ですので、相手の2ndサーブポイント率が3~4%低下していることがわかります。錦織54%⇒50%、ジョコビッチ57%⇒54%。
・統計データ(1430試合)から重回帰分析の係数を決定
2016年のトップ100選手の試合データ(1430試合)を用いました。ちなみにこの試合データは、【テニス試合結果データベース】で公開しています。
勝者と敗者それぞれのSTATS情報がありますので、選手2人の年間平均STATSから対戦したときのSTATSデータがどうなるかを予想するためのデータが1430個あることになります。このデータを利用し、最小二乗法にて、最適な係数A1,A2,A3,A4を決定します。
参考に、pythonコードを記載します。
機械学習ライブラリであるscikit-learnを使用することで、簡単に重回帰分析を実行することができています。
(2ndサーブの係数B1,B2,B3,B4は記載しませんが同じ要領で計算して決定します。)
import pandas as pd
import numpy as np
from sklearn import linear_model
import math
df_game= pd.read_csv("T_Stats2016.csv")#csvデータ読込 年間平均STATSデータ
df_player= pd.read_csv("T_StatsAverage2016.csv")#csvデータ読込 試合の統計データ
for i in range(len(df_player)):
df_game.loc[df_game['Winner']==df_player.ix[i,['PlayerName_E']].values[0],'win_1stServe']=df_player.ix[i,['FirstServePointsWonPercentage_s']].values[0]
df_game.loc[df_game['Winner']==df_player.ix[i,['PlayerName_E']].values[0],'win_2ndServe']=df_player.ix[i,['SecondServePointsWonPercentage_s']].values[0]
df_game.loc[df_game['Winner']==df_player.ix[i,['PlayerName_E']].values[0],'win_1stReturn']=df_player.ix[i,['FirstServeReturnPointsPercentage_s']].values[0]
df_game.loc[df_game['Winner']==df_player.ix[i,['PlayerName_E']].values[0],'win_2ndReturn']=df_player.ix[i,['SecondServePointsPercentage_s']].values[0]
df_game.loc[df_game['Loser']==df_player.ix[i,['PlayerName_E']].values[0],'lose_1stServe']=df_player.ix[i,['FirstServePointsWonPercentage_s']].values[0]
df_game.loc[df_game['Loser']==df_player.ix[i,['PlayerName_E']].values[0],'lose_2ndServe']=df_player.ix[i,['SecondServePointsWonPercentage_s']].values[0]
df_game.loc[df_game['Loser']==df_player.ix[i,['PlayerName_E']].values[0],'lose_1stReturn']=df_player.ix[i,['FirstServeReturnPointsPercentage_s']].values[0]
df_game.loc[df_game['Loser']==df_player.ix[i,['PlayerName_E']].values[0],'lose_2ndReturn']=df_player.ix[i,['SecondServePointsPercentage_s']].values[0]
X = df_game.loc[:, ['win_1stServe','win_2ndServe', 'lose_1stReturn', 'lose_2ndReturn']].as_matrix()
Y_1stServe=df_game['FirstServePointsWonPercentage_win'].as_matrix()
clf = linear_model.LinearRegression()#回帰分析モデルをセット
clf.fit(X,Y_1stServe)#回帰分析を実施 X⇒Y_1stServe
a = clf.coef_#係数を格納
b = clf.intercept_#切片を格納
p=clf.predict(X)#
delta=p-Y_1stServe#予測値との乖離
Xに変数となる選手Aの1stサーブポイント率、2ndサーブポイント率と選手Bの1stリターンポイント率、2ndリターンポイント率のデータを格納しています。
Y_1stServeには、その試合における選手Aの1stサーブのポイント率を格納しています。
clf.fit(X,Y_1stServe)で重回帰分析の係数決定(おそらく最小二乗法)を実施しています。
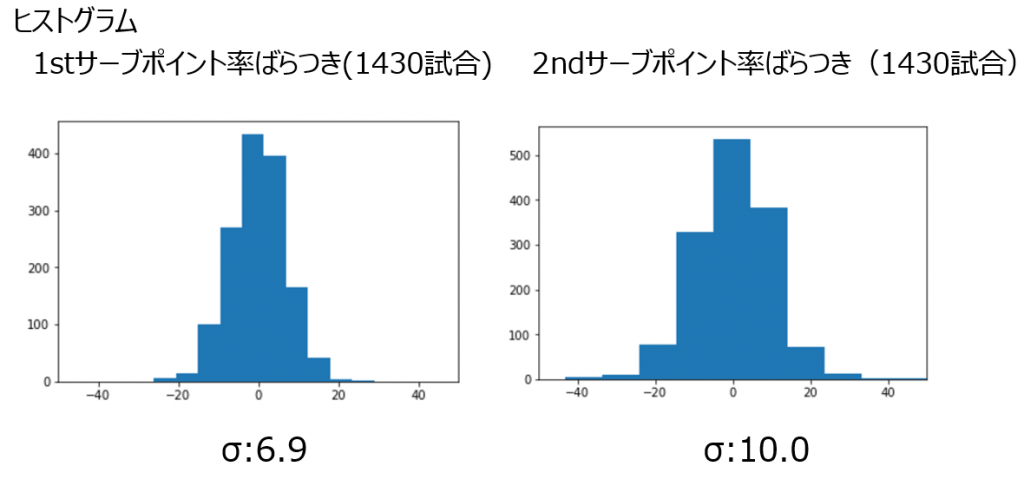
・サーブ・リターン確率のばらつきについて
あと少しわかりにくいかもしれませんが、ポイント率にばらつきが生じると考え、予測値を中心とした正規分布として毎試合ポイント率は変化するように扱います。
事実、図のヒストグラムにあるように、1430試合のデータは正規分布となりました。1stサーブポイント率と2ndサーブポイント率ですが、ポイント率はばらつくということです。要因としては、その日の調子や相手やコートサーフェスとの相性などが考えられます。
per1stServe=np.random.normal(center,sigma)
100試合計算させますが、毎試合↑のpythonコードで1stサーブのポイント率(per1stServe)を変えます。
numpy.random.normal(a,b)は平均値a、標準偏差bの正規分布となる乱数を発生させます。
center(重回帰分析で求めたポイント率)とsigma(標準偏差6.9)で乱数を発生させて1stサーブのポイント率を毎試合更新します。
これによって、試合によって調子のよいとき(ポイント率の高いとき)と悪いとき(ポイント率の低いとき)があるというばらつきを表現することができます。
・サーブ・リターン確率で全ポイントを進行させる(乱数シミュレーション)
算出したサーブ・リターン確率など各ポイントを取得する確率とサーブIN率で、試合が終了するまでプログラム上で全ポイントを進行させます。
↓はサーブポイント率が70%のときの1ポイントの進行のさせ方のコードとなります。
(実際にはサーブIn率、1stが入らなかったら2ndサーブでのポイントと組み合わせコードが増えます。全部を説明できなくてすいません。コードは最後に記載しているので参考にしてください)
import numpy as np
gamePoint=[0,0]#初期値
serve=0#0⇒Aのサーブ 1⇒Bのサーブ
winlose=np.random.randint(0,100)<70#70%以下であれば、
if(winlose):#
gamePoint[serve]+=1
else:#
gamePoint[(serve+1)%2]+=1
print(gamePoint)
Aのサーブのポイント率が70%のときで考えています。
numpy.random.randint(0,100)で、0~99の乱数を発生させます。
70より小さければAのポイントを+1とインクリメントし、70以上であれば、Bのポイントを+1とインクリメントします。
こうすることで、Aは70%の確率でポイントを獲得し、Bは30%の確率でポイントを獲得していくことになります。
これを最後のポイントまで繰り返し、どちらが勝利するかを計算します。
今後やりたいこと
トップ100全員を対戦させるとどうなるか。
精度検証(実際の結果と照らし合わせてどうなるか)
webアプリケーション化(サイトを訪れたユーザがシミュレータを扱えるようにする)
など。
やりたいことが変わったらすいません。。
・テニスの試合シミュレータをつくり、錦織とジョコビッチを1000回対戦させてみました
・テニスの試合シミュレータで2016年の1430試合の勝率を計算し、実際の戦績と比較してみました
・テニスの試合シミュレータで全米オープンの試合を予想してみました
pythonコード(試合シミュレータ)
import numpy as np
def isServeIn(perServeIn,serve):
return np.random.randint(0,100)<perServeIn[serve]
def addGamePoint(perServe,serve,gamePoint,numServe,totalServe):
totalServe[serve]+=1
winlose=np.random.randint(0,100)<perServe[serve]#0~99
if(winlose):
gamePoint[serve]+=1
numServe[serve]+=1
else:#
gamePoint[(serve+1)%2]+=1
return gamePoint
def returnGameNext(gamePoint,serve,game):
for i in range(2):
if(gamePoint[i]>3 and (gamePoint[i]-gamePoint[(i+1)%2])>1):
game[i]+=1
serve=(serve+1)%2
gamePoint[0]=0
gamePoint[1]=0
return gamePoint,serve,game
def returnTiebreakNext(gameNum,gamePoint,serve,game,status):
for i in range(2):
if(gamePoint[i]>6 and (gamePoint[i]-gamePoint[(i+1)%2])>1):
status=0
game[i]+=1
serve=(serve+1)%2
gamePoint[0]=0
gamePoint[1]=0
gameLog.append([gameNum,game[0],game[1]])
sets[i]+=1
game[0]=0
game[1]=0
return gamePoint,serve,game,status
def returnSetNext(gameNum,game,serve,sets,status):
if(game[0]==6 and game[1]==6):
status=1
else:
for i in range(2):
if(game[i]>5 and (game[i]-game[(i+1)%2])>1):
gameLog.append([gameNum,game[0],game[1]])
sets[i]+=1
serve=(serve+1)%2
game[0]=0
game[1]=0
return game,serve,sets,status
def returnFinishNext(serve,sets,status,gameWon_array):
for i in range(2):
if(sets[i]>1):
setLog.append([sets[0],sets[1]])
gameWon_array[i]+=1
#print(gameWon_array)
status=2
return status,gameWon_array
def predictPer1st(dataList):
w1st=[0.8877448,-0.20580567,-0.68625056,0.00262365]#'win_1stServe','win_2ndServe', 'lose_1stReturn', 'lose_2ndReturn'
b1st=42.2243906245
sigma1st=6.8735561550448248
predict=0
for i in range(len(dataList)):
predict+=w1st[i]*dataList[i]
predict+=b1st
return predict,sigma1st
def predictPer2nd(dataList):
w2nd=[-0.14583108,0.76162552,0.27839551,-0.92329684,0.12188441]#'win_1stServe','win_2ndServe', 'lose_1stReturn', 'lose_2ndReturn','FirstServePointsWonPercentage_win'
b2nd=55.1562816713
sigma2nd=9.9703567342698474
predict=0
for i in range(len(dataList)):
predict+=w2nd[i]*dataList[i]
predict+=b2nd
return predict,sigma2nd
nishikoriData=np.array([61,72,54,31,55])
murrayData=np.array([59,77,54,34,57])
djokovicData=np.array([65,75,57,35,58])
p1Data=nishikoriData
p2Data=djokovicData
input1_1=[p1Data[1],p1Data[2],p2Data[3],p2Data[4]]
input2_1=[p2Data[1],p2Data[2],p1Data[3],p1Data[4]]
p1_1,s1_1=predictPer1st(input1_1)
p2_1,s2_1=predictPer1st(input2_1)
input1_2=[p1Data[1],p1Data[2],p2Data[3],p2Data[4],p1_1]
input2_2=[p2Data[1],p2Data[2],p1Data[3],p1Data[4],p2_1]
p1_2,s1_2=predictPer2nd(input1_2)
p2_2,s2_2=predictPer2nd(input2_2)
#print(int(p1_1),int(p2_1),int(p1_2),int(p2_2))
#print(s1_1,s2_1,s1_2,s2_2)
per1stServeIn=[p1Data[0],p2Data[0]]
per2ndServeIn=[100,100]#データないのでいったん100%とする
num1stServe=[0,0]
num2ndServe=[0,0]
total1stServe=[0,0]
total2ndServe=[0,0]
gameWon_array=[0,0]
numGames=100
gameLog=[]
setLog=[]
for i in range(numGames):
num1stServe=[0,0]
num2ndServe=[0,0]
total1stServe=[0,0]
total2ndServe=[0,0]
status=0
gamePoint=[0,0]
game=[0,0]
sets=[0,0]
gamePoint0_array,gamePoint1_array=[],[]
game0_array,game1_array=[],[]
serve_array=[]
status_array=[]
serve=np.random.randint(0,2)
dist1_1=np.random.normal(p1_1,s1_1)
dist2_1=np.random.normal(p2_1,s2_1)
dist1_2=np.random.normal(p1_2,s1_2)
dist2_2=np.random.normal(p2_2,s2_2)
per1stServe=[dist1_1,dist2_1]
per2ndServe=[dist1_2,dist2_2]
while status<2:
if(isServeIn(per1stServeIn,serve)):
gamePoint=addGamePoint(per1stServe,serve,gamePoint,num1stServe,total1stServe)
else:
if(isServeIn(per2ndServeIn,serve)):
gamePoint=addGamePoint(per2ndServe,serve,gamePoint,num2ndServe,total2ndServe)
else:
gamePoint[(serve+1)%2]+=1
if(status==1):
gamePoint,serve,game,status=returnTiebreakNext(i,gamePoint,serve,game,status)
elif(status==0):
gamePoint,serve,game=returnGameNext(gamePoint,serve,game)
game,serve,sets,status=returnSetNext(i,game,serve,sets,status)
status,gameWon_array=returnFinishNext(serve,sets,status,gameWon_array)
gamePoint0_array.append(gamePoint[0])
game0_array.append(game[0])
gamePoint1_array.append(gamePoint[1])
game1_array.append(game[1])
serve_array.append(serve)
status_array.append(status)